Portál o technologiích a vývoji

V tomto článku o progamování základních algoritmů počítačové grafiky, si ukážeme, jak naprogramovat jednu z metod převodu barevného rozsahu obrázku do 2 barev, konkrétně metodu zvanou „Distribuce chyby“.
Princip metody je velmi jednoduchý, využívá metody prahování, tzn. je nastaven určitý práh, hodnota RGB, která pŕesáhne tento práh je nastavena na černou a hodnota, která je pod ním na bílou.
Až potud je postup stejný jako u metody prahování.

Metoda distribuce chyby však pokračuje dál, vypočítáme si chybu, které jsme se dopustili a tu pak „rozdistributujeme“ po okolnich, dosud nezpracovanych pixelech. Existuje mnoho distribučních schémat, my využijeme tzv. Floyd–Steinbergovo schéma.

1. Vytvoříme si nový obrázek typu BufferedImage. (Umožňuje nám pracovat s jednotlivými pixely).

novy = new BufferedImage(obrazek.getWidth(), obrazek.getHeight(), obrazek.getType());

2. Vytvoříme si matici o velikosti původního obrázku (1 pixel = 1 buňka matice)

int matice[][] = new int[obrazek.getWidth()][obrazek.getHeight()];

3. Stanovíme si práh (Můžeme ho nastavit na pevno, na nějakou hodnotu, nebo volitelně, třeba přes jSlider)

int prah = 150;

4. Deklarujeme si další pomocné proměnné:

int rbg;  // sem ulozime hodnotu RGB
int puvodni;  // zde bude hodnota kterou budeme porovnavat s prahem
int chyba = 0; // sem budeme ukladat vypocitanou chybu
int hod; // zde bude chyba rozpoditana podle Floyd–Steinbergova algoritmu.
int r, g, b; // jednotlive slozky pro RBG

5. Nyni jiz nasleduji cykly, vlozim sem cely kod a dole si jej vysvělíme.

 for (int i = 0; i < obrazek.getWidth(); i++) {
            for (int j = 0; j < obrazek.getHeight(); j++) {
                rbg = obrazek.getRGB(i, j);
                r = (rbg & 0xFF0000) >> 16;
                g = (rbg & 0xFF00) >> 8;
                b = (rbg & 0xFF);

                puvodni = (int) Math.round((r * 0.299) + (g * 0.587) + (b * 0.114));
                puvodni -= matice[i][j];

                if (puvodni > prah) {
                    Color barva = Color.WHITE;
                    novy.setRGB(i, j, barva.getRGB());
                    chyba = 255 - puvodni;
                } else {
                    Color barva = Color.BLACK;
                    novy.setRGB(i, j, barva.getRGB());
                    chyba = 0 - puvodni;
                }

                if (obrazek.getWidth() > (i + 1)) {
                    hod = 7 * (chyba / 16);
                    matice[i + 1][j] += hod;
                }

                if ((obrazek.getWidth() > (i + 1)) && (obrazek.getHeight() > (j + 1))) {
                    hod = 1 * (chyba / 16);
                    matice[i + 1][j + 1] += hod;

                }

                if (obrazek.getHeight() > (j + 1)) {
                    hod = 5 * (chyba / 16);
                    matice[i][j + 1] += hod;
                }

                if ((0 < (i - 1)) && (obrazek.getHeight() >; (j + 1))) {
                    hod = 3 * (chyba / 16);
                    matice[i - 1][j + 1] += hod;
                }
            }
        }

Řádky 3 až 6 slouží k zjištění barevných složek RGB.
Na řádku 8 uložíme hodnotu RGB do hodnoty puvodni v 256 odstínech šedi. Na dalším řádku odečteme od „původní“ hodnotu matice na radku i a sloupci j. (V buňce je distribuovaná hodnota podle Floyd-Seintberga).

Řádky 11 až 19 jsou defacto aplikací metody prahování + zjišťují hodnoty chyby.
Řádky 22 až 43 hlídají, aby se nezapisovalo mimo matici (IndexOutOfBounds) a ukladaji prislusne hodnoty do matice. (Distributují chybu).

Algoritmus vyjádřený maticově (matice znázorňuje okolní pixely):

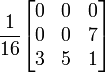
Jak vidíte tak distribuce probíhá následovně:
1. Chyba je vynásobena 1/16
2. Do buňky matice napravo od upravovaného (i+1) vložíme hodnotu (chyba / 16) * 7
3. matice[i][j+1] vložíme (chyba / 16) * 5
4. matice[i+1][j+1] (chyba / 16) * 1
5. matice[i-1][j+1] (chyba / 16) * 3
Víze k Floyd-Steinbergově algoritmu například zde:
http://en.wikipedia.org/wiki/Floyd–Steinberg_dithering

Ukázka výsledku metody: