Portál o technologiích a vývoji

Fergusonova (Hermitovská) křivka je jednou z nejčastěji používaných aproximačních křivek. Narozdíl od Bezierovi křivky neni zadana 4 body, ale dvoumi řídícími body (P0 a P1) a dvoumi tečnými vektory (P’0 a P’1). Křivka vychází z bodu P0 ve sméru vektoru P’0 a končí v bodě P1 ve směru vektoru P’1.

Křivka je vyjádřena touto rovnicí:
P(t) = P0F1(t) + P1F2(t) + P0’F3(t) + P1’F4(t)

Kde F1 až F4 jsou tzv. Hermitovské polynomy, tyto polynomi vypočteme podle následujících vzorců:
F1(t) = 2t^3 – 3t^2 + 1
F2(t) = -2t^3 + 3t^2
F3(t) = t^3 – 2t^2 + t
F4(t) = t^3 – t^2

t = <0;1> Čím více výpočtů v tomto intervalu provedeme, tím hladší bude výsledná křivka.

Nyní se již podíváme na samotný zdrojový kód:
1. Deklarujeme si proměnné

  
    int bod = 0;
    int bodyX[];
    int bodyY[];
    int bodyFergusonX[];
    int bodyFergusonY[]; 

2. Alokujeme deklarovná pole

      
        bodyX = new int[4];
        bodyY = new int[4];
        bodyFergusonX = new int[10];
        bodyFergusonY = new int[10]; 

3. V metodě MousePressed (popřípadě MouseClicked) vykreslíme body a mezi X-ovými a Y-ovými souřadnicemi 2 a 4 bodu vykreslíme úsečku, jedná se o vektory. Když máme zadané všechny body, zavoláme metodu vykresliFerguson(), která nám vypočítá a vykreslí kŕivku ze zadaných bodů.

int prumer = 4;
        Graphics g = getGraphics();
        g.setColor(Color.red);

        if (bod < 4) {
            g.drawOval(evt.getX() - prumer / 2, evt.getY() - prumer / 2, prumer, prumer);
            g.fillOval(evt.getX() - prumer / 2, evt.getY() - prumer / 2, prumer, prumer);

            bodyX[bod] = evt.getX();
            bodyY[bod] = evt.getY();
            bod++;

            if (bod == 4) {
                g.setColor(Color.blue);
                g.drawLine(bodyX[0], bodyY[0], bodyX[1], bodyY[1]);
                g.drawLine(bodyX[2], bodyY[2], bodyX[3], bodyY[3]);
                g.setColor(Color.red);
                g.drawString("P0", bodyX[0] + 5, bodyY[0] + 5);
                g.drawString("P'0", bodyX[1] + 5, bodyY[1] + 5);
                g.drawString("P1", bodyX[2] + 5, bodyY[2] + 5);
                g.drawString("P'1", bodyX[3] + 5, bodyY[3] + 5);
                vykresliFerguson();
            }
        } 

4. V metodě vykresliFerguson() si deklarujeme proměnné:

     double f1, f2, f3, f4;  // pro Hermitovké polynomy
        float t = 0; // t = <0;1>
        int zacatekX; // pro zaverecne vykresleni krivky
        int zacatekY;
        int konecX;
        int konecY; 

5. Vypočítáme si vektory P'0 a P'1 jako rozdíl zadaných bodů

     int vekt1x = bodyX[1] - bodyX[0];
        int vekt1y = bodyY[1] - bodyY[0];

        int vekt2x = bodyX[3] - bodyX[2];
        int vekt2y = bodyY[3] - bodyY[2]; 

6. V cyklu počítáme Hermitovské polynomy a násobíme jimy zadané body, výsledkem jsou body křivky, které si ukádáme do polí.

       for (int i = 0; i < 10; i++) {
            t = (i + 1) / (float) 10;
            f1 = 2 * Math.pow(t, 3) - 3 * Math.pow(t, 2) + 1;
            f2 = -2 * Math.pow(t, 3) + 3 * Math.pow(t, 2);
            f3 = Math.pow(t, 3) - 2 * Math.pow(t, 2) + t;
            f4 = Math.pow(t, 3) - Math.pow(t, 2); 

            bodyFergusonX[i] = (int) Math.round(bodyX[0] * f1 + bodyX[2] * f2 + vekt1x * f3 + vekt2x * f4);
            bodyFergusonY[i] = (int) Math.round(bodyY[0] * f1 + bodyY[2] * f2 + vekt1y * f3 + vekt2y * f4);

        } 

7. Nakonec kŕivku vykreslíme

  zacatekX = bodyX[0];
        zacatekY = bodyY[0];
        konecX = bodyFergusonX[0];
        konecY = bodyFergusonY[0];

        for (int i = 1; i < 11; i++) {
            g.drawLine(zacatekX, zacatekY, konecX, konecY);
            
            if (i != 10) {
                zacatekX = konecX;
                zacatekY = konecY;
                konecX = bodyFergusonX[i];
                konecY = bodyFergusonY[i];
            }
        } 

Křivka může vypadat nějak takto (V závisloti na zadaných bodech):

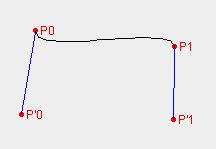
Nastíněné řešení je zvoleno tak, aby bylo snadno pochopitelné, optimálnějším řešením by možná bylo souřadnice uchovávat v objektu typu point a vkládat do ArrayListu.

Zdroj: http://lubovo.misto.cz/_MAIL_/curves/ferguson.html