Beziérova křivka je jedna ze základních aproximačních křivek (= křivka neprochází zadanými body, ale snaží se jim co nejvěrnějsi přiblížit. Algoritmus pro Bezierovu křivku je poměrně snadný, k výpočtu hodnot (bodů, osa x a osa y) využívá tzv. Bernsteinovy polynomy. My si ukážeme jak vypočítat a nakreslit křivku 3 řádu. Základem je tedy stanovení 4 bodů, které v tomto případě necháme vybrat uživatele.
1. deklarujeme si 4 pole, 2 typu int pro x-ové a y-ové souřadnice „naklikaných bodů“ a dvě typu float pro x-ové a y-ové souřadnice samotné křivky (podle nich se bude vykreslovat).
Velikosti polí bodyKrivkyX a bodyKrivkyY můžete nechat uzivatele regulovat, více výpočtů bodů udělá křivku hladší.
bodyX = new int[4];
bodyY = new int[4];
bodyKrivkyX = new float[11];
bodyKrivkyY = new float[11];
2. Uživatelem „naklikané“ body si uložíme do příslušných polí, například v události MouseClicked, zároveň si hlídáme aby uživatel skutečně naklikal jen 4 body. V místě kliknutí můžeme například vykreslit kroužek s pořadovým číslem.
int prumer = 3;
if (kliknuto < 4) {
bodyX[kliknuto] = evt.getX();
bodyY[kliknuto] = evt.getY();
g.setColor(Color.red);
g.drawOval(evt.getX() - prumer, evt.getY() - prumer, prumer, prumer);
g.fillOval(evt.getX() - prumer, evt.getY() - prumer, prumer, prumer);
g.drawString("" + kliknuto, evt.getX() + 3, evt.getY() + 3);
kliknuto++;
}
3. Následně hlídáme stav, kdy budou zadány 4 body, pokud již jsou, zavoláme příslušné metody, jejich účel je myslím dobře zřetelný z názvu:
if (kliknuto == 4) {
vypocetKrivky();
nakresliKrivku();
}
4. Výpočet kŕivky je část nejsložitější a k jejímu vyhotovení je nutné umět vypočítat kombinační čísla a pochopit princip tvorby Bersteinových polynomů. Pro křivku 3. řádu jsou však výpočty velmi snadné a není problém je zjednodušit:
B1 = (1-t)^3
B2 = 3t * (1-t)^2
B3 = 3t^2 * (1-t)
B4 = t^3
Velikost t (kroky <0,1>) a s tím související počet vypočítávaných bodů určují hladkost výsledné křivky.
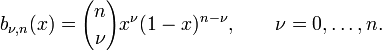
public static void vypocetKrivky() {
float t = 0;
float b1 = 0;
float b2 = 0;
float b3 = 0;
float b4 = 0;
for (int i = 0; i < 11; i++) {
t = (float) (i * 0.1);
b1 = (1 - t) * (1 - t) * (1 - t);
b2 = 3 * t * ((1 - t) * (1 - t));
b3 = 3 * t * t * (1 - t);
b4 = t * t * t;
bodyKrivkyX[i] = b1 * bodyX[0] + b2 * bodyX[1] + b3 * bodyX[2] + b4 * bodyX[3];
bodyKrivkyY[i] = b1 * bodyY[0] + b2 * bodyY[1] + b3 * bodyY[2] + b4 * bodyY[3];
}
}
Vypočteme si Bernsteinovy polynomy pro křivku 3. řádu a potom plníme pole cyklem hodnotami sočtu bodů vynásobených polynomem.
5. Máme li naplněné pole udávající souřadnice křivky, nebrání nám nic tomu, abychom ji vykreslili, k tomu můžeme využít například nasledujici metodu:
public void nakresliKrivku() {
Graphics g = getGraphics();
for (int i = 0; i < 10; i++) {
g.drawLine((int) bodyKrivkyX[i], (int) bodyKrivkyY[i], (int) bodyKrivkyX[i + 1], (int) bodyKrivkyY[i + 1]);
}
}
Kŕivka je tímto vykreslena, jako doplněk bývají často body propojeny přimkou nebo se uživateli umožňuje zadání počtu zadávaných bodů a tím se křivka rozšíří na křivku vyššího řádu. Výsledek může vypadat například takto:
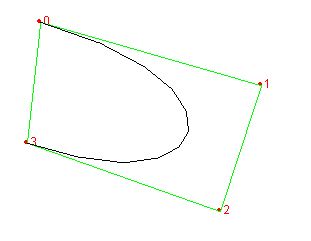
Zdroj: http://cs.wikipedia.org/wiki/Bernsteinův_polynom

Žádné komentáře