Lagrangeova křivka patří k nejstarším pokusům o spojení bodů křivkou. Jedná se o interpolační křivku (narozdíl od Fergusonovi a Bezierovi křivky, které jsou aproximační), tzn. že prochází přímo zadanými body. V našem připadě dovolíme uživateli zadat libovolných, předem zadaný, počet bodů. Existuje i možnost vykreslovat křivku znovu pokaždé, kdy uživatel zadá další bod, tato úprava je velmi snadná a jistě ji zvládné dopsat do ukázaného algoritmu každý.
1. Nejprve necháme uživatele zadat počet bodů, po jejichž zadnaní se má křivka vykreslit, k tomu můžeme využít například komponentu jTextField. Následně v metodě mousePressed vykreslujeme body a ukládáme jejich souřadnice do ArrayListu.
Pro správné vykreslení křivky musí body splňovat podmínku že xi musí být menší než xi+1 (xi < xi+1) (toto zde pro jednoduchost neošetřuji, ale stačilo by přidat jednu podmínku, takto je správnost vykreslení z části ponechána na svědomí uživatele).
private void formMousePressed(java.awt.event.MouseEvent evt) {
Graphics g = getGraphics();
int prumer = 5;
g.setColor(Color.red);
if (nakreslenoBodu < pocetBodu) {
Point p = new Point(evt.getX(), evt.getY());
body.add(p);
g.drawOval(p.x - prumer / 2, p.y - prumer / 2, prumer, prumer);
g.fillOval(p.x - prumer / 2, p.y - prumer / 2, prumer, prumer);
g.drawString("P" + nakreslenoBodu, evt.getX() + 6, evt.getY() + 6);
nakreslenoBodu++;
}
if (nakreslenoBodu == pocetBodu) {
vykresliLagrange();
}
}
Pokud je počet nakreslených bodů shodný s počtem plánovaných bodů, zavoláme metodu, která vypočte a vykreslí křivku.
2. Nyní si představíme slíbenou metodu pro výpočet křivky, ten celý vychází ze vzorce pro výpočet Lagrangevova polynomu, který je zde uveden.
public int vypoctiLagrange(double x) {
double citatel, jmenovatel, soucet = 0.0;
Point bod = new Point();
for (int i = 0; i < body.size(); i++) {
bod = body.get(i);
citatel = 1.0;
jmenovatel = 1.0;
for (int j = 0; j < body.size(); j++) {
if (i != j) {
citatel = citatel * (x - body.get(j).x);
jmenovatel = jmenovatel * (bod.x - body.get(j).x);
}
}
soucet = soucet + bod.y * (citatel / jmenovatel);
}
return soucet;
}
3. Vykreslení křivky probíhá v metodě vykresliLagrange()
Graphics g = getGraphics();
int y;
ArrayList bodyLagrang = new ArrayList();
for (int x = 0; x < getWidth(); x++) {
y = vypoctiLagrange(x);
bodyLagrang.add(new Point(x, y));
}
int xpoints[] = new int[bodyLagrang.size()];
int ypoints[] = new int[bodyLagrang.size()];
for (int i = 0; i < bodyLagrang.size(); i++) {
xpoints[i] = bodyLagrang.get(i).x;
ypoints[i] = bodyLagrang.get(i).y;
}
g.drawPolyline(xpoints, ypoints, xpoints.length);
}
Jak vidíte, nejprve jsme si vytvořili nový ArrayList kam budeme ukládat souřadnice výsledné křivky, následně generujeme tyto body v cyklu, do y přiřadíme výsledek metody vypoctiLagrange() a do x přiřazujeme index cyklu, který jede od začátku do samého konce kreslícího plátna. (Křivka není vodorovná úsečka, proto nebude "od kraje ke kraji", ale jedná se o ideální počet bodů pro správné vykreslení).
Samotnou křivku můžeme vykreslit takto:
int xpoints[] = new int[bodyLagrang.size()];
int ypoints[] = new int[bodyLagrang.size()];
for (int i = 0; i < bodyLagrang.size(); i++) {
xpoints[i] = bodyLagrang.get(i).x;
ypoints[i] = bodyLagrang.get(i).y;
}
g.drawPolyline(xpoints, ypoints, xpoints.length);
a nebo takto:
for (int i = 0; i < bodyLagrang.size()-1; i++) {
g.drawLine(bodyLagrang.get(i).x, bodyLagrang.get(i).y, bodyLagrang.get(i+1).x, bodyLagrang.get(i+1).y);
}
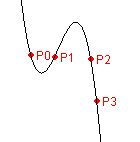
Záleží čistě na vašich preferencích. Výsledek bude vypadat podobně jako na tomto obrázku (v závisloti na zadaných bodech):

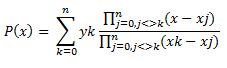
Žádné komentáře