Portál o technologiích a vývoji

Dnes si naprogramujeme aplikaci, která nám bude ořezávat úsečky o hrany konvexního mnohoúhelníku. Využijeme k tomu algoritmu Liang-Barsky. Algoritmus je založen na tom, že hrany obdélníkového okna mají triviální normály.

1. Nejprve si náhodně vygenerujeme úšečky, aby bylo co ořezávat, k tomu využijeme funkci Random() z knihovny java.util.Random, kterou je nejprve potřeba importovat. Úsečky samozřejmně můžeme zadávat i jinak, ale tento způsob je na ukázku nejrychlejší.

 import java.util.Random;

2. Deklarujeme si globálně tyto proměnné:

    int x1, y1, x2, y2;
    int x_orezane1, y_orezane1, x_orezane2, y_orezane2;
    Rectangle rect;

3. Aby se nám úsečky generovali ihned po spuštění programu, budeme vše kreslit v „přepisované (overriding)“ metodě
paintComponent(), v netBeans si ji můžeme nechat vygenerovat (ALT + INSERT, Override Method -> JComponent a tam ji již najdete). Její obsah si doplníme nějak takto:

  @Override
    protected void paintComponent(Graphics g) {
        super.paintComponent(g);

        Random rand = new Random();
        for (int i = 0; i < 500; i++) {
            x1 = Math.abs(rand.nextInt() % getWidth());
            y1 = Math.abs(rand.nextInt() % getHeight());
            x2 = Math.abs(rand.nextInt() % getWidth());
            y2 = Math.abs(rand.nextInt() % getHeight());

            g.setColor(Color.red);
            g.drawRect((int) rect.getX(), (int) rect.getY(), (int) rect.getWidth(), (int) rect.getHeight());

            g.setColor(Color.black);
            g.drawLine(x1, y1, x2, y2);


            if (orezUseckuLiangBPravouhelnikem(x1, y1, x2, y2, rect) == true) {
                g.setColor(Color.cyan);
                g.drawLine(x_orezane1, y_orezane1, x_orezane2, y_orezane2);
            }
        }
    }

4. Voláme tedy metodu orezUseckuLiangBPRavouhelnikem(), metodu sem vložím celou a na konci si ji vysvětlíme:

private boolean orezUseckuLBPravouhelnikem(int x1, int y1, int x2, int y2, Rectangle hranice) {

       int dx = x2 - x1;
        int dy = y2 - y1;


        float p1 = -dx;
        float p2 = dx;
        float p3 = -dy;
        float p4 = dy;

        float q1 = x1 - hranice.x;
        float q2 = hranice.x + hranice.width - x1;
        float q3 = y1 - hranice.y;
        float q4 = hranice.y + hranice.height - y1;

        float[] p = {p1, p2, p3, p4};
        float[] q = {q1, q2, q3, q4};


        float u1 = 0, u2 = 1, r = 0;

        for (int i = 0; i < 4; i++) {

            if ((p[i] == 0) && (q[i] < 0)) {
                return false; //vynechame
            }

            if (p[i] != 0) {
                r = q[i] / p[i];
                if (p[i] < 0) {
                    u1 = Math.max(u1, r);
                } else if (p[i] > 0) { //p[i] > 0
                    u2 = Math.min(u2, r);
                }
            }
        }

        x_orezane1 = (int) Math.round(x1 + u1 * dx);
        y_orezane1 = (int) Math.round(y1 + u1 * dy);

        x_orezane2 = (int) Math.round(x1 + u2 * dx);
        y_orezane2 = (int) Math.round(y1 + u2 * dy);


        if (u1 < u2) {
            return true;
        } else {
            return false;
        }
    }

Vstupními hodnotami jsou:
x1 tj. začátek původní úsečky X // možno nahradit například proměnnou datového typu Point (Point z => z.x, z.y atd.)
y1 tj. to samé pro Y
x2 tj. konec původní úsečky X
y2 tj konec původní úsečky Y

hranice je objekt typu Rectangle, který si vytvoříme například v konstruktoru (rect = new Rectangle(25, 25, 150, 150);)

Nyní si musíme spočítat p a q podle následujících vzorců:

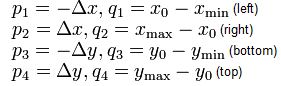
vypočtené hodnoty si uložíme do polí dat. typ float.

Dodatečné informace:
Jestliže p = 0 => úsečka je rovnoběžná
jestliže p < 0 => úsečka směřuje dovnitř mnohoúhelníku
Jestliže p > 0 => úsečka směřuje z mnohoúhelníku ven

Nyní si deklarujeme další pomocné proměnné, u1 = 0, u2 = 1 a r = 0, jsou to konstatní defaultní hodnoty pro úsečku.

V cyklu (v našem případě se jedná o čtverec, počítáme u1 (v případě p<0), u2 (p>0)a r (r = q / p) úsečky pro které platí p = 0 a zároveň q < 0 je možno vynechat, jsou rovnoběžné s ořezávanou oblastí a leží před ní. Následných výpočtem zjistíme nové hodnoty x a y ořezaných úseček. A nakonec vrátíme true (u1 < u2) nebo false (u1 > u2).

Výsledek bude vypadat takto:

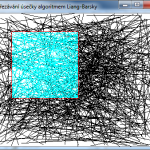
Dodatek:
Posunování ořezávané oblasti (v našem případě čtverce) tažením myši.

 private void formMouseDragged(java.awt.event.MouseEvent evt) {
        if ((rect.x <= evt.getX()) && (rect.getWidth() + rect.x >= evt.getX()) && (rect.y <= evt.getY()) && (rect.getHeight() + rect.y >= evt.getY())) {
            rect.setLocation(evt.getX() - ((int) rect.getWidth() / 2), evt.getY() - ((int) rect.getHeight() / 2));
            repaint();
        }
    }

Nesmíme si akorát zapomenou hlídat, jestli úvodní kliknutí proběhlo do ořezávané oblastni, k tomu slouží ta podmínka.