Bresenhamův algortimus je jedním ze základních algoritmů pro vykreslování dvourozměrných objektů do rastrové mřížky. Na rozdíl od algoritmu DDA by měl být rychlejší, využívá totiž celočíselnou aritmetiku (DDA využívá desetinných čísel, které jsou před vykreslením zaokrouhleny, což zbytečně zabírá čas). Bresenhamuv algoritmus využívá tzv. predikce, která laicky řečeno rozhoduje, která z nasledujících možností vykreslení bodu se doopravdy vykreslí.
Vstupními parametry Bresenhamova algoritmu pro rasterizaci úsečky jsou počáteční (x1, y1) a koncové souřadnice (x2,y2). Pokud využíváme událost, můžeme je v Javě vyčíst pomocí metod getX() a getY() z parametru evt.
1. Nejprve si tedy zjistíme počáteční a koncové souřadnice úsečky:
x1 = evt.getX(); // pocatecni zjistit napriklad v MousePressed
y1 = evt.getY();
x2 = evt.getX(); // koncove zjistit napriklad v MouseReleased
y2 = evt.getY();
2. Deklarujeme si proměnné pro kroky na ose x a ose y
int stepX, stepY;
3. Dále stanovíme dx, dy (delta, rozdíl) a x,y jenž budou mít nyní hodnotu počátečního bodu:
int dx = x2 - x1;
int dy = y2 - y1;
int x = x1;
int y = y1;
4. Podle toho zda-li je dx, dy < 0 nebo ne, určujeme + nebo - smer na ose x a ose y.
if (dx < 0) {
dx = -dx;
stepX = -1;
} else {
stepX = 1;
}
if (dy < 0) {
dy = -dy;
stepY = -1;
} else {
stepY = 1;
}
5. Následně vykreslíme počáteční bod (Java neumožňuje kreslit bod, proto si jej nahradime usečkou se shodnými pocatečními a koncovými body).
Graphics g = getGraphics();
g.drawLine(x1, y1, x1, y1);
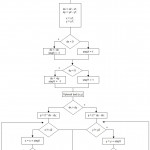
6. Nyní se dostáváme k samotnému počítání algoritmu:
if (dx > dy) { //osa x
int p = 2 * dy - dx;
while (x != x2) {
x += stepX;
if (p > 0) {
y += stepY;
p += 2 * dy - 2 * dx;
} else {
p += 2 * dy;
}
g.drawLine(x, y, x, y);
}
} else { // osa Y
int p = 2 * dx - dy;
while (y != y2) {
y += stepY;
if (p > 0) {
x += stepX;
p += 2 * dx - 2 * dy;
} else {
p += 2 * dx;
}
g.drawLine(x, y, x, y);
}
}
Nejprve je nutné vybrat takzvanou řídící osu, dx nebo dy. V závislosti na vybrané ose se počítá predikce (pro každou je jiný vzorec, prohozený rozdíl dx a dy).
Počáteční predikce pro osu X se počítá podle vzorce: 2 * dy – dx;
Počáteční predikce pro osu Y se počítá podle vzorce: 2 * dx – dy;
V závislosti na vybrané ose se spustí cyklus (dokud x =! x2), nebo (dokud y != y2) tzn. dokud neni dosaženo koncového bodu. K hodnotě X se přičte hodnota kroku X (popřípadě ekv. u varianty s řídící osou Y).
Následně se vyhodnocuje predikce, je li věčí než 0, k y (ekv. k x) přičti krokY (ekv. krokX) a vypočítej novou predikci.
Pro X-ovou osu se počítá predikce:
Jestliže předchozí > 0: predikce = predikce + 2 * dy – 2 * dx
Jestliže předchozí < 0: predikce = predikce + 2 * dy;
Pro Y-ovou osu se počítá predikce:
Jestliže předchozí > 0: predikce = predikce + 2 * dx – 2 * dy;
Jestliže předchozí < 0: predikce = predikce + 2 * dx;

Žádné komentáře